Computing History
Introduction
A computer is a tool for taking over difficult mental tasks that humans are not good at, such as storing large amounts of information and doing complex or repetitive calculations. Although humans can do these tasks, they are prone to making mistakes and are fairly slow. For many tasks, such as building reliable bridges, scheduling air travel, and analyzing weather data, we need tools that can store millions of numbers and do complex calculations with them thousands of times a minute. Let’s look briefly at the development of these tools and why we ended up with the computers we've got today.
The Difference Engine
In the years around 1800, people increasingly said: we've got difficult, dangerous, repetitive physical tasks that are really hard on humans, let's create machines -- tools that can take over these tasks and do them faster and better, without getting injured. This was called the industrial revolution.
Once using machines to do physical tasks was starting to be
widespread, mathematicians such as Charles Babbage, noted that there are also
many repetitive, difficult mental
tasks to deal with. For example, solving
many engineering problems (like building all those other machines!) requires
plugging numbers into long polynomials and getting out a correct result, which
was a long and tedious problem for humans, who would sometimes get the wrong
results.
Babbage designed a machine called the Difference Engine, which could calculate polynomials. Suppose we have the polynomial -5x2+99x-1782 and we need to know what it comes out to for 100 different values of x; the Difference Engine, once it was set up for this polynomial, would work its way through all the values and show the results.
Babbage said, after explaining his idea to Parliament in order to ask for money, “On two occasions I have been asked, — ‘Pray, Mr. Babbage, if you put into the machine wrong figures, will the right answers come out?’ I am not able rightly to apprehend the kind of confusion of ideas that could provoke such a question.” People who know little about how computers work have always had trouble understanding what they can and can’t do!
Babbage also worked on a design for a more general-purpose machine he called the Analytical Engine. Babbage corresponded with the community of mathematicians and showed them his design; one of these was Ada Lovelace. Based on his design, she outlined a series of steps-- settings for the engine -- that would result in a more complex result than just a table of values for one polynomial. It would have required a human to set up the machine for each step and put the results together; the Difference Engine wasn’t designed to follow the steps on its own.
This was the beginning of the idea of hardware and software. The physical parts of a computing machine are its hardware; we build these to have basic capabilities. But to do anything really useful and interesting, we would have to combine these capabilities in some order to create a result. Creating a step-by-step process to do this is called programming. A program — software — is a process that uses the built-in capabilities of the hardware to achieve a more complex result.
Unfortunately, Lovelace never got to run her programs, because Babbage never managed to get the complete Difference Engine built[2]. But now the idea was out there and in the 1800s similar devices started to appear.
From Single to General Purpose Computing Machines
After Babbage, single-purpose computing machines were built more and more frequently. For instance, there was a US census at 1900, and they used a machine called the Hollerith Tabulating Machine to add up the numbers.
A single-purpose computing machine can only do one kind of task. The Difference Engine could calculate polynomials, but couldn’t add up census data. The Hollerith Tabulating Machine could add up census data, but couldn’t calculate polynomials. If you needed to do both, then you would have to buy and store two different machines. If you needed to do another task, you’d have to buy another machine. Typically only governments could afford such machines.
During World War II, the Enigma Machine used by the German military took messages and encrypted them — put them into a code. Almost all codes are not difficult to crack, instead they take so long to work through because of the repetitive calculations required, that it isn’t worth trying. The Enigma Machine could do more repetitive operations when encrypting the message than a human could, which meant that cracking it took much longer than something encrypted by a human.
One of the people working on breaking the Enigma code for the Allied side was Alan Turing, a mathematician. Like many others in the mathematical community, Turing was interested in the idea of general purpose computers.
Instead of having a single purpose computer for each job, you would have a general purpose computer, and as new jobs came up, you would tell this one computer how to do each of them. This is much more convenient than having to have a different machine for every task; instead you can just have one. But you do need to then tell the machine how to do each task, instead of having the task built in, and you have to build in basic abilities that can be put together to do many different tasks.
Turing worked out a formal, mathematical system for describing general purpose computers. His theoretical computer, the Turing Machine, is the basis of computer science. A Turing machine is not a physical machine, but a mathematical description of a perfect computer — the computer that can do anything any other computer can do, without limits of what hardware we could ever actually build in the real world. This is important because, if we can prove mathematically that you can't solve a certain problem with a Turing Machine — the perfect computer — then we know no other computer, no matter how powerful, can do it either.
For example, you have probably experienced having a computer program freeze while you were working. Now you have two options, wait and hope that it will eventually start working again, or assume it is frozen forever and close it probably losing your work. If only you knew for sure whether to give up or not! Why isn’t there another program you could use every time to tell whether this freeze is temporary or permanent? We can prove, using the Turing machine, that it is not possible to create a program that can tell if any other program is frozen forever, so we know we shouldn’t waste our time trying to write such a program.[4]
Data and Instructions

As part of the Turing machine, Turing came up with a way of describing anything a computer could do, based on two kinds of information: data and instructions.
The data are any values we need to store while doing the task, including the ones we start with and any we find along the way, particularly any final result.
The instructions are the series of steps to go through to process those numbers. These steps must be basic capabilities that are built into the computer.
So, for instance, if you needed to find the maximum of a group of numbers, then those numbers are data, and the maximum, the result we are trying to find, is also data. Instructions might include storing the first number as our maximum, and comparing each number in turn to the current maximum, replacing the maximum if the new number is bigger.
Storage and Processing

So, since we need data in our general purpose computing machine, we need a place in the machine to put it: a storage area. And we need the computer to follow our instructions, so we need it to have a part that can do basic operations like adding, subtracting, comparing to see which of two numbers is bigger, etc.
We call the part that can follow instructions the processor.
Suppose I'm finding maxima of various lists of numbers. Do I really want to enter the instructions to do this again and again every time I have different data? No, I’m far too lazy to do that, so we'll need to store not only the data, but the instructions too.
After the end of the war[5], Turing was working on the design of a real, physical computer with processor, storage for data, and storage for instructions. At this point, there were different opinions in the mathematical community (part of which was becoming the computer science community) on whether we should have separate storage for the two things or not.
In 1951, Turing was arrested. After his house was burgled, he had admitted to a police officer that he was dating a young man. He was eventually offered the choice between prison and chemical castration. About two years later he died — probably suicide. Turing was only 40 and he could certainly have continued making contributions to computer science for decades. In August, 2014, Alan Turing was given a royal pardon by Queen Elizabeth[6].
But the work went on. In the United States, John von Neumann[7] worked on the EDVAC project, a computer that had one part for processing, and one part that stored both data and instructions together, in the same way. All digital computers since are based on this stored program machine (also known as a von Neumann machine).
Accelerating Technology

In 1950, a computer was an enormous object. You didn't walk into the room with your computer, you walked into your computer, which took up the whole room. The basic component computers were built from was the vacuum tube, which was large and complex and expensive to build. These computers were mostly owned by governments or big businesses because they were so expensive. In the years since, we have made our computers smaller, faster, and cheaper.
Eventually, vacuum tubes were replaced by much smaller, cheaper components called transistors. Computers built from smaller, cheaper pieces could be smaller, cheaper computers. But we were still building computers by creating thousands of these transistors and assembling them, an expensive, time consuming process.
At the start of the 1970s, a new approach was found – integrated circuits. This allowed the transistors to be created all as one piece, in a single process, at microscopic size.
The resulting hardware was so small they were called microprocessors. And, amazingly, the integrated circuit process not only made the computers smaller, but even cheaper to build. For the first time, we could build computers you could actually fit on a desk, and that were affordable for personal use. They have continued getting smaller since.
Although certainly people started buying computers to do necessary tasks, they also wanted to be able to play games on the computer. Computer games grew more popular, and then something strange happened: game consoles came out. A game console is a computing machine that does only one kind of task: it plays games. It isn’t designed for doing word processing or spreadsheets. We are back to single-purpose computing machines!
Why, when that means we have to buy more than one kind of
computer? Some tasks, such as certain kinds of calculation used for graphics,
could be done through a process using simple general operations, but could also
be built-in with specialized hardware. So
if we don’t have to compromise to provide general capabilities to do a variety
of tasks, we can build a single purpose computer that is particularly good at the
one task it does, and do it more cheaply than building a general purpose
computer that is very good at this one task and also good at everything else it needs to do.
In addition to the advances in hardware, we have made advances in software. The Operating System is the program (examples are Microsoft Windows 10, or Mac OS X 10.7 Lion) that is in charge of everything on the computer. In the 1980s and 1990s, many advances were made in designing operating systems and other programs that were friendlier for people to use, encouraging even more people to buy home computers.
A network is a system of computers that can communicate with each other. Although the beginnings of the ideas that would later be used to create the internet were already coming together in the 1960s, it was in the 1990s that a global network of computers that communicated with each other became reality. Our networking abilities have continued to advance, often spurred by the difficulties of dealing with this huge-scale network that was cobbled together through trial and error before we knew what we were doing.
Moore’s Law
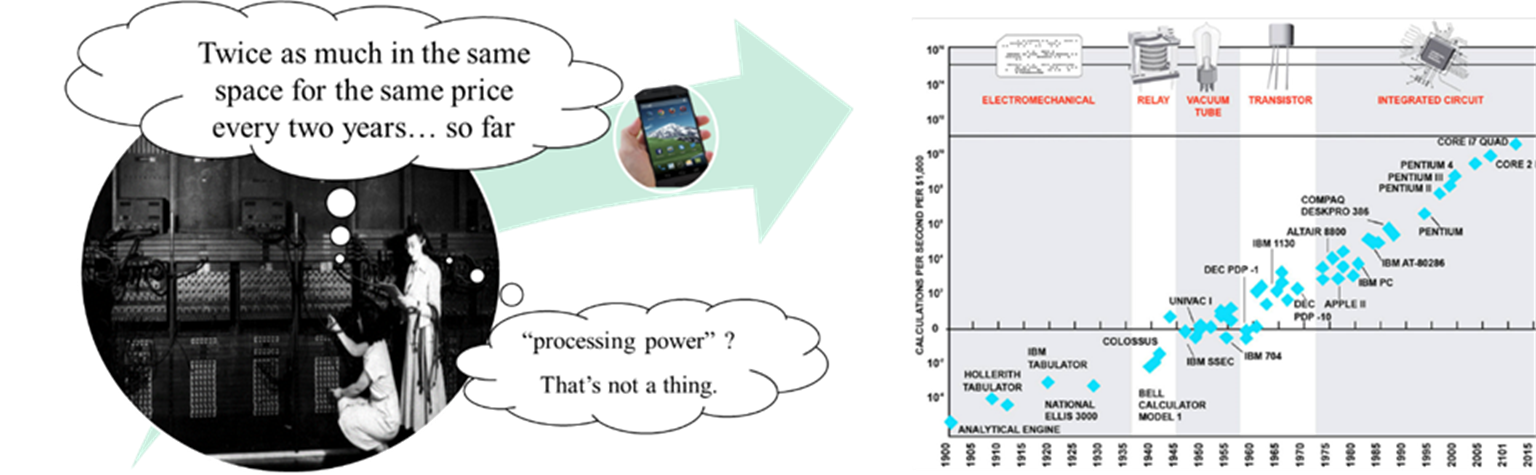
Moore's law is an observation made by Gordon Moore: the number of transistors we were able to manufacture to fit in the same space at the same price has doubled roughly every two years.
Note that this is an observation about the past not a physical law that determines the future[9]. Hardware companies have taken this “law” to heart and try to time things to this schedule.
Other people noticed that there have been similar patterns for our advances in speed, graphics, and other aspects of computing technology.
People in the media who don’t know what the law actually says often talk about “processing power” or the “power of a computer” doubling every two years. But computer “power” is an advertising term with no real meaning, so it doesn’t make sense to talk about doubling it.
Integrated Circuits
With integrated circuits, a whole component of a computer can be made in one piece out of one material. How?
This material must be something that can sometimes be an insulator – not letting electricity through – and sometimes a conductor – letting electricity through like a wire. This kind of material that can act both ways is called a semiconductor, and how it acts depends on how we chemically treat it.
The process for creating a component the integrated circuit way is to first take our semiconductor and cover it in a protective film that keeps any chemical from getting through, but which breaks up when subjected to UV light.
A mask is like a stencil that has holes where the conductor parts of the component should be. A light is flashed through the mask onto the film, making parts of the film break down so that some areas of the semiconductor are still protected, but others are open.
Then we chemically treat it, and the areas the chemicals touch have their electrical properties changed.
So essentially, an entire component of a computer can be made by the process: film, flash, spray with chemicals. (For real components, this will probably be repeated a few times.) In fact, we can make many copies of the same component at once by this method on one big slice of semiconductor, and just cut them out afterwards. So the process is very fast. It is also relatively cheap. And we can make the components as small as we can make the holes in the mask.
Storage and Binary

We needed to store information in a computer, but how? Electronic components respond to electricity – either electricity ON or electricity OFF. That’s all we have to go on, so we will have to find a way to store information with just those two possibilities.
Power OFF is generally used
to mean no, and power ON to mean yes.
So, if we had some situation for which we needed to store yes, we could
light up one electronic component with power, walk away, come back later, and
find the component still ON – successfully storing a yes. Similarly we could turn that component OFF,
walk away, come back, find it OFF, and have successfully stored a no. So now we have figure out how to store something
in electronic form.
We also use OFF to store the
number 0 and ON to store the number 1.
So, suppose someone stored a 1 by turning a component ON. I could then come by later, check the
component, and find out that they had stored 1.
(Same goes for storing 0 by turning the component OFF.)
So now we have a way of
storing the number 0 and the number 1 in a computer!!!
Which is as far as we ever
got.
Modern computers are able to
store the number 0 and the number 1, and that’s it. That’s all.
The computer you’re reading this on can only store 0’s and 1’s.
But it turns out that’s
enough to store any number. Decimal
numbers use only 0,1,2,3,4,5,6,7,8,9, but does that mean we can’t store numbers
higher than 9? No, we just put those
symbols together in longer patterns to represent larger numbers. After 9 we go to two-digit patterns: 10, 11,
12,…, 98, 99. Once we run out of two-digit patterns, we go to three digits.

We can do the same even if we
only have 0 and 1. We just have to go to
longer patterns sooner. Numbers based on
just 0 and 1 are called binary numbers. After 0 and 1, the next number in
binary is spelled 10. That’s how we
spell “ten” in decimal, but it’s how we spell “two” in binary. So for two digits we have 10, 11, and then we
have to go to three digits.
For any number you choose,
there is a binary pattern (just 0’s and 1’s).
For large numbers, these patterns are very long. Every binary pattern represents a number.
The math to convert between binary and decimal is fairly simple. Think of how decimal numbers are written. 1010 in decimal means we have one thousand, no hundreds, one ten, and no ones: (1 * 1000) + (0 * 100) + (1 * 10) + (0 * 1). Each place in the number is a power of 10.
In binary, instead of thousands, hundreds, and tens, the
places in a number are based on powers of two: 2, 4, 8, 16, etc. So 1010 in binary means one eight, no fours, one two, and no
ones: (1 * 8) + (0 * 4) + (1 * 2) + (0 * 1).
Don’t forget: We write binary
patterns with the symbols 0 and 1, but inside the computer, these are instead
ONs and OFFs. You can picture a pattern
storing a number inside the computer as a row of little lights, some of which
are ON and some OFF.
Now we know how to store
numbers. But what about everything
else? We will have to reuse our binary
patterns to mean more than one thing. The
same pattern might sometimes represent
·
a number
·
a letter
·
the amount of red
at one point in a picture
·
the pitch of a
sound
·
an instruction to
tell the computer one step in doing a task
·
…
For instance, the pattern
01000001 is used for both the number 65 and the letter capital A.
Based on the context, the
computer knows how to interpret the pattern at any given time. For instance a pattern in a .mp3 file would
be interpreted as sound but the same pattern used in a .docx file might be
interpreted as text.
Processing

The part of the computer that does processing is called the CPU. We have a similar problem for processing as we did for storage. How do we build something electronic that can perform even a very simple mental task without a brain????
The basic electronic components we can build are called gates. You can picture them as a box with two[10] wires coming in and one[11] coming out. Suppose the wires going in are A and B, and the wire coming out is C. There are four possibilities for A and B:
· both OFF
· A OFF and B ON
· A ON and B OFF
· both ON
For each of these possibilities, we need to decide whether the gate should turn the output, C ON or OFF in that case.
Example: Adding Binary
Here’s an example of how much thinking has to go into designing hardware to do even something that seems very simple: Suppose we use A and B to represent two numbers that we’re adding, and the result, C should be the sum A+B. Remember that OFF is 0 and ON is 1.
· 0+0=0, so if A and B are both OFF, we want to turn C OFF
· 0+1=1 so if A is OFF and B is ON, we want to turn C ON
· 1+0=1 so if A is ON and B is OFF, we want to turn C ON
What if both are ON? 1+1=10 which is a two digit number, so if A and B are both ON C should be OFF, but this shows we also need to add more wires and another gate to handle a carry. The carry gate would have the same A and B going in, but be set up to always output OFF unless A and B are both ON, and our result would include both C and the wire from this new gate.
So, we can figure out how to set up gates to add one digit binary numbers. To add longer numbers, we’ll have to do this for each digit (and handle a carry from the previous digit). So even for just adding, things get fairly complex pretty fast.
Instructions and Machine Language
For every ability we want to build into our computer, someone has to figure out what the gates should look like to combine binary patters and achieve that goal. This is why the capabilities that can be built into a CPU tend to be very simple – adding, subtracting, copying patterns, etc. Anything more complex must be built up from these very simple abilities.
The part of the CPU that actually does such operations is the ALU, the arithmetic logic unit.
For each capability in the CPU of a computer there must be a binary pattern used to indicate that we want to do that as the next step of our task. These are called the instructions. A program to do anything interesting will be made up of thousands and thousands of instructions.
The list of instructions that a CPU understands are called its machine language. Different kinds of computer have different machine languages.
You can imagine wires running from each binary ON/OFF in the instruction register to different parts of the CPU so the instruction can tell the ALU, data registers, etc what they should do. In fact, in real computers things are more complex and there is a whole extra component of the CPU called the control unit that deals with decoding the meaning of each instruction and setting the CPU to respond correctly, but that is outside the scope of this course.
Input and Output
 A computer that can store and
process data technically does what we want, but isn’t
useful to us unless we have a way to get information into and out of it. Since the computer needs everything to be in
binary, and almost no humans like to work in binary, we need input devices to
translate information coming in into a form the computer can use, and output
devices to translate information coming out into a human-friendly form.
A computer that can store and
process data technically does what we want, but isn’t
useful to us unless we have a way to get information into and out of it. Since the computer needs everything to be in
binary, and almost no humans like to work in binary, we need input devices to
translate information coming in into a form the computer can use, and output
devices to translate information coming out into a human-friendly form.
A keyboard is a fairly simple input device. You press a key with the letter you want on it, and the binary pattern for that letter is sent into the computer’s storage. Most input devices have a much harder job.
Anything stored in a computer must be in digital form, that is, it must be a list of discrete values (that is, individual numbers). But most things in the world aren’t lists of values. They aren’t lists of anything. Most of the world is analog – continuous information.
Sampling
 Consider,
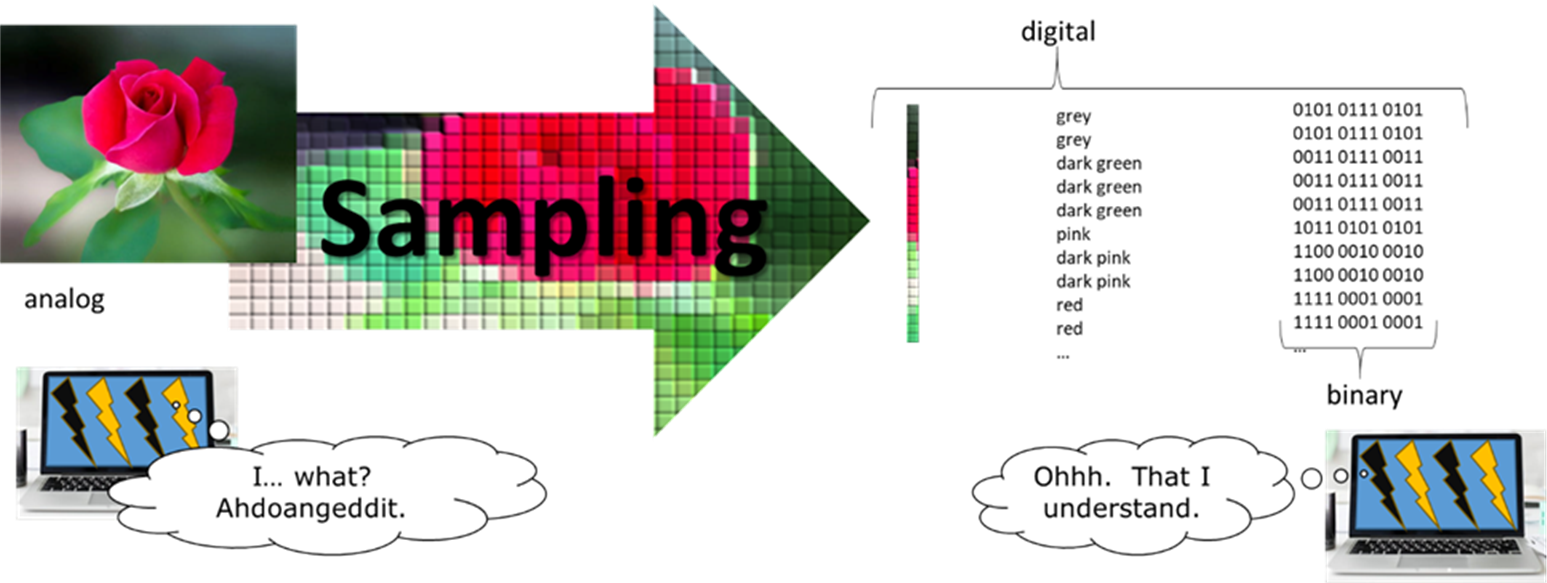
for instance, a picture of a flower.
That picture isn’t a list, but if we want to store it in the computer,
we need a way to convert it into one.
The standard way to convert from analog to digital is sampling – break the analog information
into small pieces, and then record a value for each piece.
Consider,
for instance, a picture of a flower.
That picture isn’t a list, but if we want to store it in the computer,
we need a way to convert it into one.
The standard way to convert from analog to digital is sampling – break the analog information
into small pieces, and then record a value for each piece.
For the picture, we can cut it into small squares, and record the color at the center of each square. A standard way to store a color in a computer is to have three numbers saying how much red, how much green, and how much blue are in the color. So the squares in the middle of the picture would be stored with high values for red and low for green and blue. (In the computer, of course, these numbers are stored as binary patterns.)
Cutting the picture into a fairly small number of squares resulted in something that doesn’t look much like the original picture. To get closer to the original, we could divide it into more pieces, but notice that this will make our list of numbers much longer. Analog information can always be divided into smaller pieces to get more detail, so by definition sampling is always leaving out some of the information in the original analog.
We could sample sound by recording the pitch and volume at every millisecond, or the motion of a mouse by recording the x and y position every millisecond.
Note that all of the following are digital, in different formats:
· A B C format: Latin alphabet
· 1 2 3 format: decimal
· 011 101 100 format: binary
To be stored in the computer, information must be digital, stored in binary format.
Once we have the information stored, the computer can process it, but to do us any good we then need it converted back to a form we can understand, using an output device such as a monitor or speaker. The processes for turning a list of values back into something a human can appreciate are just as complicated as what we have to do to get the data into the computer in the first place.